- Compute the residuals of regressing the response
variable against the indpendent variables but omitting
Xi
- Compute the residuals from regressing Xi
against the remaining indpendent variables.
- Plot the residuals from (1) against the residuals from (2).
Velleman and Welsch (see References below) express this mathematically as:
- Y.[i] versus
Xi.[i]
where
- Y.[i] = residuals from regressing
Y (the response variable) against all the indpendent
variables except Xi
Xi.[i] = residuals from regressing Xi against the remaining indpependent variables.
Velleman and Welsch list the following useful properties for this plot:
- The least squares linear fit to this plot has the slope
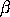 i and intercept zero.
i and intercept zero.
- The residuals from the least squares linear fit to
this plot are identical to the residuals from the
least squares fit of the original model (Y against
all the independent variables including
Xi).
- The influences of individual data values on the
estimation of a coefficient are easy to see in this plot.
- It is easy to see many kinds of failures of the model or violations of the underlying assumptions (nonlinearity, heteroscedasticity, unusual patterns).
===> 선형성 진단에도 쓸수 있다. (acprplot이 더 적합하지만)
http://www.itl.nist.gov/div898/software/dataplot/refman1/auxillar/partregr.htm
'통계 , 수학' 카테고리의 다른 글
| 로짓, 프로빗 결과의 해석 (1) (odds ratio) (0) | 2017.08.09 |
|---|---|
| [통계, stata 학습 자료 / 사이트] (0) | 2017.08.09 |
| 회귀분석 진단하기 (with STATA) - 잔차의 정규분포성(normality of risiduals), 이분산성(heteroscadasticity of variance of risiduals), 다중공선성(multicolinearity in dependant variables), 선형성(linearity) (0) | 2017.08.08 |
| 회귀분석 진단하기 (with STATA) - 아웃라이어의 진단과 처리 (0) | 2017.08.08 |
| 다중회귀분석의 가정들 (0) | 2017.08.07 |

댓글